Autor: Ștefan-Cosmin Dăscălescu
Cunoștințe necesare
- Vectori (tablouri unidimensionale) ● ● ● ● ●
- Variabile și tipuri de date simple ● ● ● ● ●
- Algoritmi de sortare ● ● ● ● ●
Soluția problemei rufe (OJI 2019, clasele XI-XII)#
Link problemă
Această problemă poate fi accesată aici.
Pentru a rezolva această problemă, ne putem gândi mai întâi la o soluție înceată, care va calcula pentru fiecare punct distanța de la punctul central la toate celelalte puncte, le ordonează crescător și ia cele mai mari \(k\), afișând distanța corespunzătoare.
Totuși, această abordare este foarte înceată și nu ne va aduce punctajul maxim. Astfel, vom vrea să ne gândim la optimizări. În primul rând, o idee pe care o putem explora este aceea că dacă ne gândim la o linie sau o coloană, distanța de la origine la punctele de pe acea linie/coloană sunt mai întâi descrescătoare, iar mai apoi crescătoare, cu punctul paralel cu originea fiind cel mai apropiat de aceasta.
Această distribuție a distanțelor ne duce cu gândul la a reprezenta aceste regiuni ale matricii, împărțind astfel suprafața în patru zone, pentru care putem simplifica răspunsurile foarte mult, după modelul de mai jos.
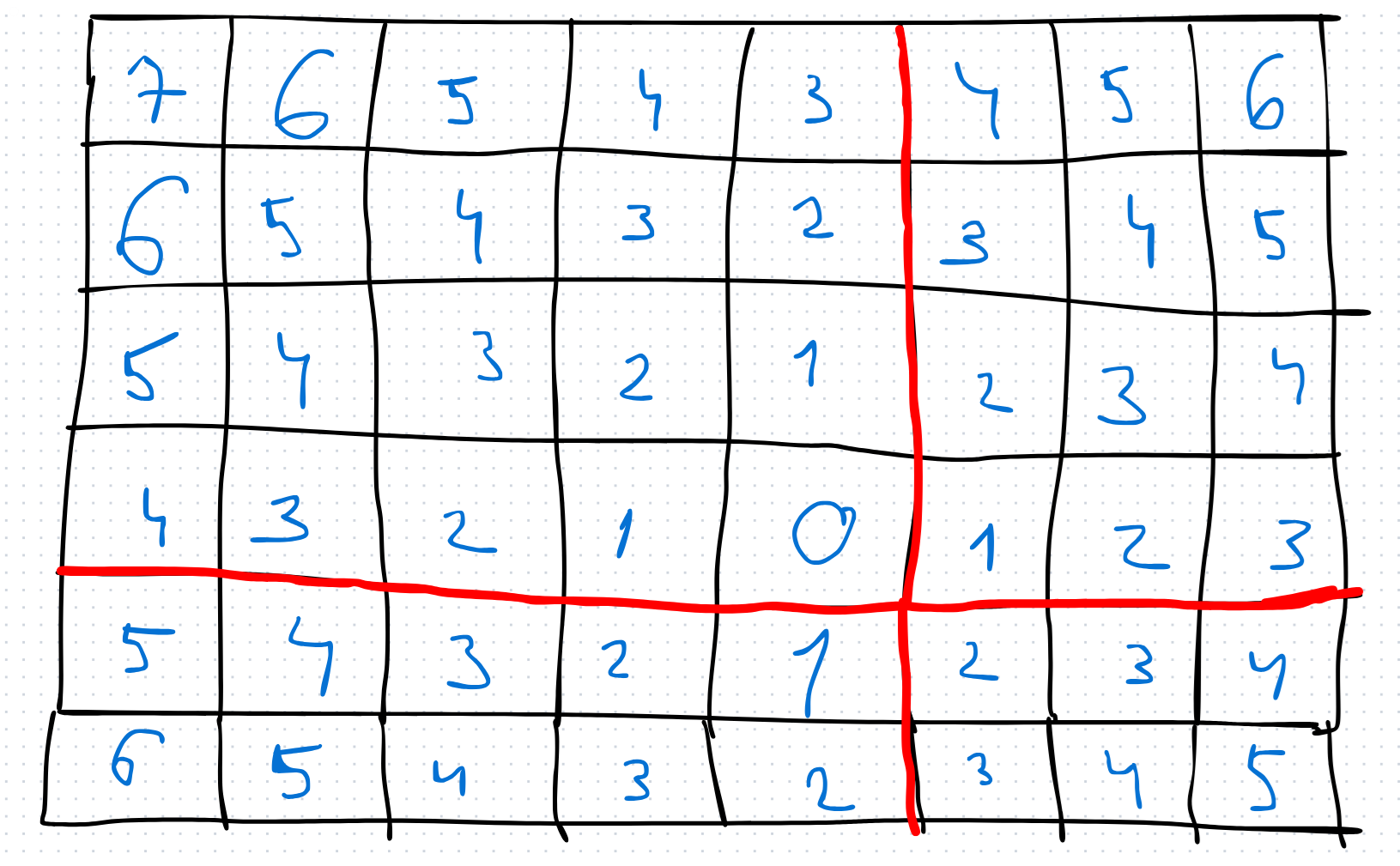
Apoi, deoarece cu cât ne apropiem mai mult de origine, vom acoperi tot mai multe puncte, ne putem gândi la o căutare binară pe răspuns, scopul nostru este să aflăm numărul de puncte aflate la o distanță mai mare decât valoarea țintă.
Deoarece am împărțit în patru regiuni, este îndeajuns să aflăm aria suprafețelor acoperite, care se reduce la aria unor triunghiuri cu puncte în jurul colțurilor cele mai îndepărtate, un exemplu fiind arătat mai jos.
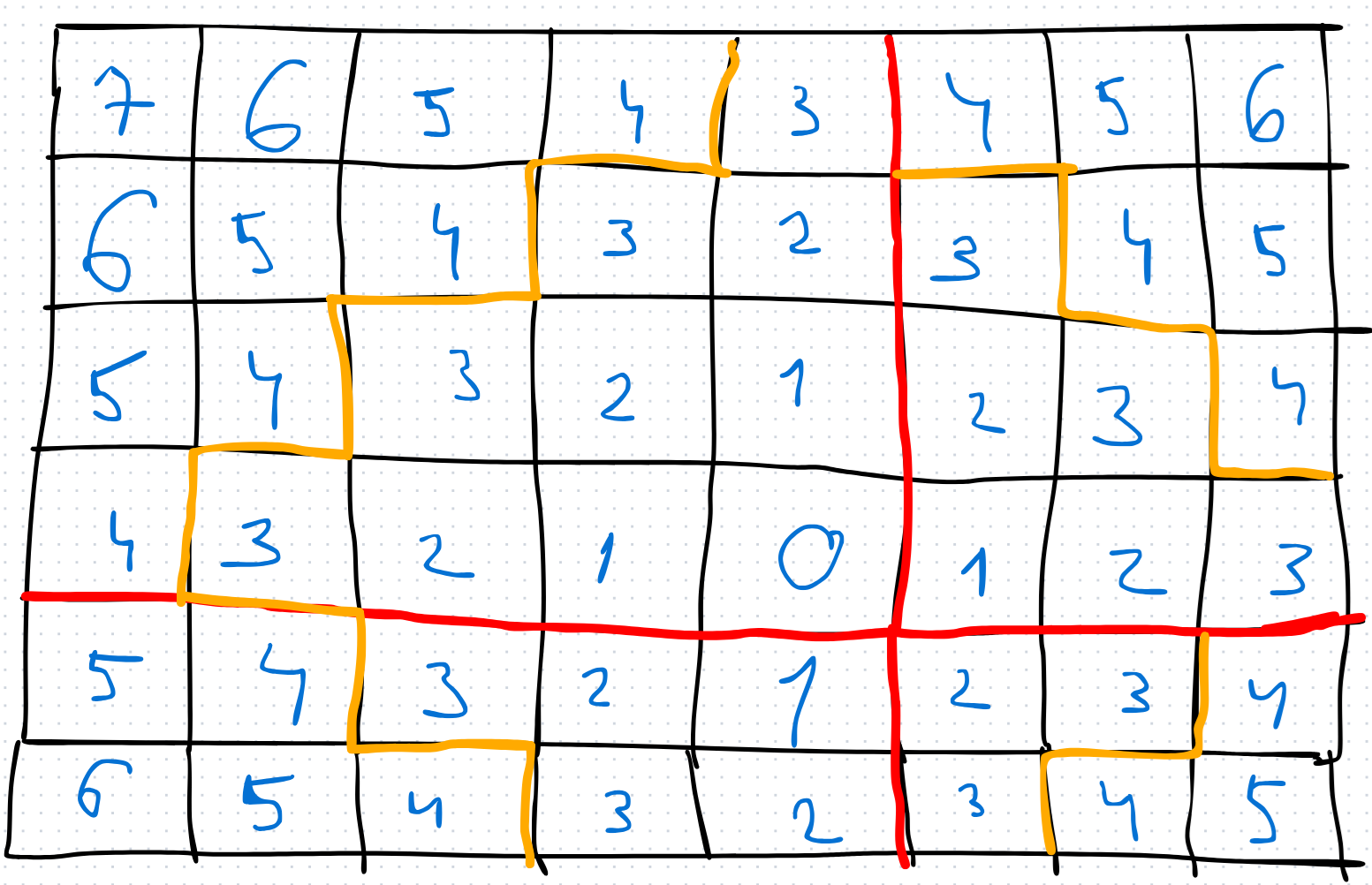
Folosind formulele pentru aria unui triunghi dreptunghic (mai multe detalii puteți găsi în implementare, numărul de cazuri necesare devine mult mai mic, implementarea devenind mult mai facilă).
Astfel, soluția voastră va rula în timp logaritmic, fiind îndeajuns de rapidă pentru obținerea celor 100 de puncte.
Mai jos puteți găsi o soluție neoficială care ia punctajul maxim.
#include <fstream>
struct Rect {
long long cornerVal;
int height, width;
};
int N, M, A, B;
long long K;
Rect rects[4];
long long tri(long long n) {
return n * (n + 1) / 2;
}
bool check(long long val) {
long long total = 0;
for (int i = 0; i < 4; i++) {
long long cornerVal = rects[i].cornerVal;
long long height = rects[i].height;
long long width = rects[i].width;
if (cornerVal < val) {
continue;
}
long long dist = cornerVal - val + 1;
long long cur = tri(dist);
if (dist > height) {
cur -= tri(dist - height);
}
if (dist > width) {
cur -= tri(dist - width);
}
total += cur;
}
return (total >= K);
}
int main() {
std::ifstream cin("rufe.in");
std::ofstream cout("rufe.out");
cin >> N >> M >> A >> B >> K;
rects[0] = {A + B - 2, A - 1, B - 1};
rects[1] = {A + (M - B) - 1, A - 1, (M - B) + 1};
rects[2] = {(N - A) + B - 1, (N - A) + 1, B - 1};
rects[3] = {(N - A) + (M - B), (N - A) + 1, (M - B) + 1};
long long low = 0, high = 2e9;
while (low < high) {
int mid = (low + high + 1) / 2;
if (check(mid)) {
low = mid;
}
else {
high = mid - 1;
}
}
cout << low << "\n";
}