Ciurul lui Eratostene

Ce este ciurul lui Eratostene?

Ciurul lui Eratostene este o metodă eficientă de afla toate numerele prime între 1 și $n$, folosindu-ne de proprietățile corespunzătoare numerelor naturale, precum și de relațiile dintre divizori și multipli. Pe lângă aplicația sa principală, se va dovedi a fi un algoritm foarte util pentru foarte multe tipuri de precalculări care sunt centrate în jurul aflării divizorilor sau a altor valori ce se calculează în funcție de divizorii numerelor de la 1 la $n$.

Pentru a afla numerele prime de la 1 la $n$, vom avea un algoritm simplu, care va lua la rând numerele de la 2 la $n$ și pentru fiecare număr nemarcat de la 2 la $n$, se vor marca toți multiplii acestuia. Astfel, numerele nemarcate sunt numerele prime, acestea nefiind marcate anterior de momentul accesării lor, iar numerele marcate sunt numerele compuse. Se remarcă faptul că 1, nefiind număr prim, nu este luat în considerare.

Să exemplificăm algoritmul pentru numerele de la 2 la 30. Voi descrie doar pașii ce exemplifică ce se întâmplă când avem de-a face cu numere prime.

• La pasul $i = 2$, 2 este marcat drept număr prim, iar acesta va marca numerele pare de la 4 la 30 drept compuse $(4, 6, 8, 10, 12, 14, 16, 18, 20$, $22, 24, 26, 28, 30)$.
• La pasul $i = 3$, 3 este marcat drept număr prim, iar acesta va marca numerele multiplu de 3 de la 6 la 30 drept compuse $(6, 9, 12, 15, 18, 21, 24, 27, 30)$.
• La pasul $i = 5$, 5 este marcat drept număr prim, iar acesta va marca numerele multiplu de 5 de la 10 la 30 drept compuse $(10, 15, 20, 25, 30)$.
• La pasul $i = 7$, 7 este marcat drept număr prim, iar acesta va marca numerele multiplu de 7 de la 14 la 30 drept compuse $(14, 21, 28)$.
• La pasul $i = 11$, 11 este marcat drept număr prim, iar acesta va marca numerele multiplu de 11 de la 22 la 30 drept compuse $(22)$.
• La pasul $i = 13$, 13 este marcat drept număr prim, iar acesta va marca numerele multiplu de 13 de la 26 la 30 drept compuse $(26)$.
• La pașii $i = 17$, $i = 23$, $i = 29$, 17, 23 și 29 sunt marcați drept numere prime, dar multiplii lor mai mari ca ei sunt mai mari ca 30, nemaifiind marcați drept numere compuse, chiar dacă sunt, deoarece nu fac parte din scopul rulării algoritmului nostru pentru numerele până la 30.

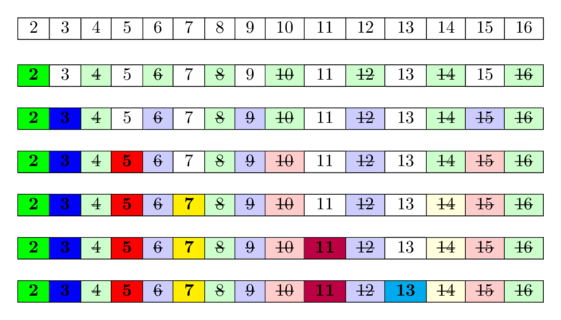
Un exemplu de vizualizare pentru numerele de la 1 la 16

Algoritmul se dovedește a fi o optimizare față de metoda standard de aflare pentru toate numerele de la 1 la $n$ a primalității, complexitatea devenind $\mathcal{O}(n \log \log n)$ pentru aflarea primalității pentru toate numerele, respectiv $\mathcal{O}(n \log n)$ pentru majoritatea celorlalte tipuri de prelucrări. De asemenea, și implementarea se dovedește a fi una foarte scurtă, ciurul putând fi scris în câteva rânduri.

int prim[100001];
for (int i = 2; i <= n; i++) {
    if (prim[i] == 0) {
        for (int j = i + i; j <= n; j += i) {
            prim[j] = 1;
        }
    }
}

Optimizări ale implementării

Deși algoritmul în sine este deja foarte rapid, în practică concurenții tind să aplice diverse optimizări de constantă inspirate din optimizările ce se pot aplica algoritmului de aflare a divizorilor unui număr $n$. Printre altele, putem vorbi de începerea celui de-al doilea for de la $i^2$ (primul număr compus care nu a fost marcat anterior va fi mereu $i^2$) sau de procesarea lui 2, urmată de procesarea numerelor impare din 2 în 2.

int prim[100001];
for (int i = 4; i <= n; i += 2) {
    prim[i] = 1;
}
for (int i = 3; i <= n; i += 2) {
    if (prim[i] == 0) {
        for (int j = i * i; j <= n; j += i * 2) {
            prim[j] = 1;
        }
    }
}

int prim[100001];
for (int i = 4; i <= n; i += 2) {
    prim[i] = 1;
}
for (int i = 3; i * i <= n; i += 2) {
    if (prim[i] == 0) {
        for (int j = i * i; j <= n; j += i * 2) {
            prim[j] = 1;
        }
    }
}

// afisarea numerelor prime de la 1 la n
for (int i = 2; i <= n; i++) {
    if (prim[i] == 0) {
        cout << i << " ";
    }
}

Chiar dacă aceste implementări nu îmbunătățesc semnificativ performanța ciurului lui Eratostene, ele pot fi utile în contextul optimizărilor ce ar putea fi folosite la rezolvarea problemelor.

Alte aplicații ale ciurului lui Eratostene

După cum am menționat la începutul articolului, ciurul lui Eratostene este un algoritm foarte versatil, putând fi folosit pentru aflarea multor proprietăți ale numerelor, precum divizorii (primi sau toți) ai unui număr, pentru calcule de tipul celor folosite la pinex sau Möbius și așa mai departe. Câteva din implementările acestor operații vor fi prezentate mai jos, în cadrul problemei educaționale descrisă în cele ce urmează.

Problema Ciurul lui Eratostene

View Problem

Kilonova

Could not fetch problem details

Deschide

Se dau $q$ operații de forma $type \ value$. În funcție de tipul operației, va trebui să faceți următoarele lucruri:

• $1\ value$: Să se afișeze Prime sau Composite dacă numărul este prim, respectiv compus.
• $2\ value$: Să se afișeze divizorii primi ai lui $value$, în ordine crescătoare. Dacă $value = 1$, se va afișa o linie goală.
• $3\ value$: Să se afișeze divizorii lui $value$, în ordine crescătoare.

Pentru a rezolva problema (și în general pentru a rezolva problemele care implică folosirea ciurului lui Eratostene), ne vom precalcula toate răspunsurile folosind variații ale ciurului lui Eratostene, una pentru numerele prime și cealaltă pentru divizori în general. Pentru a ține în memorie toți divizorii, vom folosi varianta din STL a vectorilor, deoarece face accesarea datelor mai ușoară.

#include <iostream>
#include <vector>

using namespace std;

const int NMAX = 1000000;
int q, prime[NMAX + 1];
vector<vector<int> > divisors, prime_divisors;

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);

    divisors.resize(NMAX + 1);
    prime_divisors.resize(NMAX + 1);

    for (int i = 1; i <= NMAX; i++) {
        for (int j = i; j <= NMAX; j += i) {
            divisors[j].push_back(i);
        }
    }

    prime[1] = 1;
    for (int i = 2; i <= NMAX; i++) {
        if (prime[i] == 0) {
            for (int j = i; j <= NMAX; j += i) {
                prime_divisors[j].push_back(i);
                if (j != i) {
                    prime[j] = 1;
                }
            }
        }
    }

    cin >> q;

    for (int i = 1; i <= q; i++) {
        int type, value;
        cin >> type >> value;
        if (type == 1) {
            cout << (prime[value] == 0 ? "Prime" : "Composite") << '\n';
        }
        if (type == 2) {
            for (int j = 0; j < (int)prime_divisors[value].size(); j++) {
                cout << prime_divisors[value][j] << " ";
            }
            cout << '\n';
        }
        if (type == 3) {
            for (int j = 0; j < (int)divisors[value].size(); j++) {
                cout << divisors[value][j] << " ";
            }
            cout << '\n';
        }
    }
    return 0;
}

Problema Cufăr

View Problem

Kilonova

Could not fetch problem details

Deschide

Vrăjitoarea cea bună are un cufăr în care este închisă piatra magică de către piticii lăzii cu ajutorul unui cifru digital. Piticii i-au dat vrăjitoarei o cutie în care sunt $n$ cartonașe. Pe fiecare cartonaș este scris un număr natural pe care vrăjitoarea îl va folosi să deschidă lada. Valorile scrise pe cartonașe sunt distincte între ele.

Pentru a afla cifrul trebuie să procedeze astfel: extrage fiecare cartonaș din cutie și apoi determină valoarea magică asociată numărului natural scris pe cartonaș. Pentru fiecare cartonaș valoarea magică este dată de al $k$-lea divizor prim al numărului înscris pe acesta. Vrăjitoarea trebuie să adune valorile magice obținute pentru cele $n$ cartonașe și apoi să introducă în ordine cifrele valorii obținute, pentru a descuia lada.

Pentru a rezolva problema vom afla folosind un ciur toți divizorii primi ai numerelor mai mici sau egale cu $10^6$, aceștia fiind folosiți pentru a calcula răspunsul la query-uri. Aflarea răspunsului final devine ușoară ulterior efectuării acestui pas.

#include <fstream>
using namespace std;

ifstream f("cufar.in");
ofstream g("cufar.out");

int c, n, nr, k, prime[9][1000002];
int cate[1000002];
long long sol;
bool prim[1000002];

void ciur() {
    for (int i = 2; i <= 1000000; i++) {
        if (!prim[i]) {
            for (int j = i; j <= 1000000; j += i) {
                prim[j] = 1;
                ++cate[j];
                prime[cate[j]][j] = i;
            }
        }
    }
}

int main() {
    ciur();
    f >> c >> n;
    if (c == 1) {
        f >> nr >> k;
        g << prime[k][nr] << '\n';
    } else {
        long long sol = 0;
        for (int i = 1; i <= n; ++i) {
            f >> nr >> k;
            sol += 1LL * prime[k][nr];
        }
        g << sol << '\n';
    }
    return 0;
}

Problema primprim

View Problem

Kilonova

Could not fetch problem details

Deschide

Pentru un număr natural a definim costul ca fiind valoarea absolută (modulul) diferenței dintre a și numărul prim cel mai apropiat de a. Asupra unui șir de $n$ numere naturale, situate pe poziții numerotate de la 1 la $n$, se aplică, în ordine, o succesiune de $q$ operații. O operație constă dintr-o înlocuire și o afișare și este descrisă sub forma $i \ x \ p$, cu semnificația: mai întâi înlocuim cu $x$ elementul din șir de pe poziția $i$; apoi afișăm suma minimă totală a costurilor unor elemente convenabil selectate de pe $p$ poziții distincte din șir.

Cunoscând $n$ și cele $n$ elemente ale șirului, scrieți un program care să determine:

• suma costurilor tuturor elementelor din șirul dat;
• rezultatele afișate în urma aplicării fiecăreia dintre cele $q$ operații, date în forma precizată.

Pentru a rezolva problema, vom precalcula pentru fiecare valoare răspunsul optim pentru fiecare număr de la 1 la $a$ folosind ciurul lui Eratostene. Apoi, parcurgem valorile de la 1 la $a$ pentru a afla răspunsul optim după ce am aflat numerele prime din șir.

Pentru a rezolva query-urile, voi folosi un vector de frecventa pentru a tine aceste diferențe, care de altfel sunt destul de mici. Apoi, pentru fiecare query, voi parcurge vectorul de frecvență pentru a afla suma celor mai mici $p$ diferențe.

#include <cmath>
#include <fstream>

using namespace std;

ifstream fin("primprim.in");
ofstream fout("primprim.out");

int vals[1000002], primes[200002], cnt, ans[1100002];
bool pr[1100002];

int fr[202];

int main() {
    int c;
    fin >> c;

    int n, a = 1100000, i, j;
    fin >> n;

    for (i = 1; i <= n; i++) {
        fin >> vals[i];
    }

    // precalculam raspunsul optim pentru fiecare numar de la 1 la a folosind
    // ciurul lui Eratostene

    for (i = 2; i <= a; i++) {
        if (pr[i] == 0) {
            primes[cnt++] = i;
            for (j = i + i; j <= a; j += i) {
                pr[j] = 1;
            }
        }
    }

    int poz = -1;

    // parcurg valorile de la 1 la a pentru a afla raspunsul optim dupa ce am
    // aflat numerele prime
    ans[1] = 1;
    for (i = 2; i <= a; i++) {
        if (pr[i] == 0) {
            poz++;
        }
        ans[i] = abs(i - primes[poz]);
        if (poz + 1 < cnt) {
            ans[i] = min(ans[i], abs(i - primes[poz + 1]));
        }
    }

    // voi folosi vector de frecventa pentru a tine aceste diferente, care de
    // altfel sunt destul de mici

    for (i = 1; i <= n; i++) {
        fr[ans[vals[i]]]++;
    }

    if (c == 1) {
        int total = 0;
        for (i = 1; i <= n; i++) {
            total += ans[vals[i]];
        }
        fout << total;
        return 0;
    }

    int q;
    fin >> q;

    for (i = 1; i <= q; i++) {
        int a, b, p;
        fin >> a >> b >> p;

        fr[ans[vals[a]]]--;
        vals[a] = b;
        fr[ans[vals[a]]]++;

        int dif = 0;
        int sol = 0;

        // la fiecare pas parcurg vectorul de frecventa pana cand dau de p
        // diferente

        while (p) {
            sol += min(p, fr[dif]) * dif;
            p -= min(p, fr[dif]);
            dif++;
        }

        fout << sol << '\n';
    }
    return 0;
}

Concluzie

Ciurul lui Eratostene este una dintre cele mai importante metode de a lucra cu numere prime, precalculările care se pot face pe stilul acestui algoritm ne pot ajuta în multe contexte, în special când calculăm divizori, sume sau chiar numărul de soluții în alte probleme.

Probleme suplimentare

• CSES Counting Divisors
• CSES Common Divisors
• RoAlgo PreOJI 2024 Factoria
• Moisil++ Sprime
• infoarena numereprime
• ONI 2013 divizori
• ONI 2019 comun
• OJI 2024 Macarie
• OJI 2024 avid
• OJI 2023 Primprim
• ONI 2024 Geologie
• ONI 2013 Extraprime
• ONI 2022 Baraj Juniori Triprime
• ONI 2021 Baraj Juniori Intergalactic
• Probleme cu ciurul lui Eratostene de pe kilonova

Lectură suplimentară

• Ciurul lui Eratostene - Pbinfo
• Eratostene si alte ciururi - Pbinfo
• Ciurul lui Eratostene - CPPI Sync
• Wikipedia - Ciurul lui Eratostene
• Articol de pe CP Algorithms