Simularea soluției

De exemplu, pentru $N=8$, aplicând de $N$ ori regula $A$ se obțin șirurile: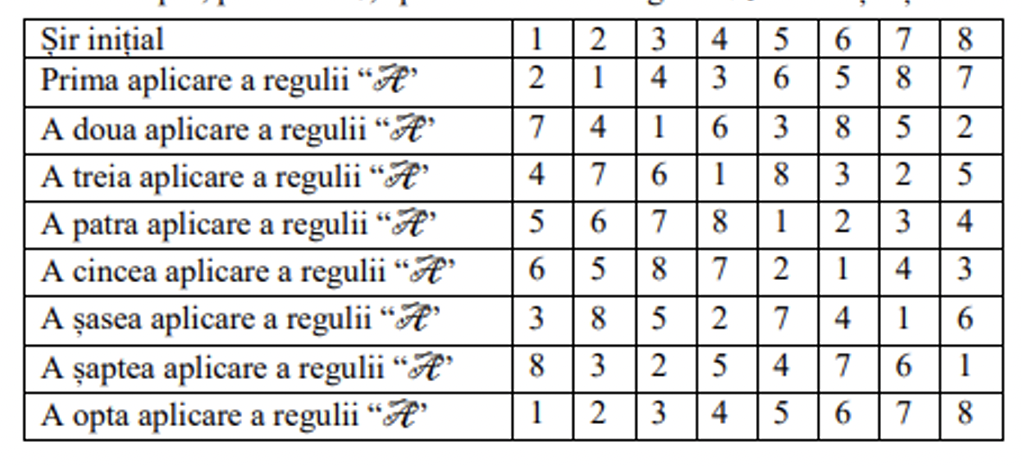

Observăm că prin aplicarea de un număr impar de ori a regulii, șirul rezultat are pe pozițiile impare numerele pare. Numere pare au apariție periodică în șirurile rezultate în ordinea $2, 4, 6, 8, 2, 4, 6, ...$ Analog, numerele impare apar pe poziții impare în ordinea $1, 3, 5, 7, 1, 3, 5, ...$ Dacă se aplică regula de un număr par de ori, pe pozițiile pare apar numerele pare.

Studiind exemplul, observăm că:

1. Dacă numărul de aplicări ale regulii date $R$ este impar, atunci dacă poziția $K$ este impară atunci numărul căutat este egal cu $(R+K)$ sau $N$ dacă acest rest este 0. Dacă poziția $K$ este pară, atunci numarul căutat este egal cu $(N+K-R)$ sau $N$ dacă acest rest este 0.

2. Dacă numărul de aplicări ale regulii $A$ date $R$ este par, atunci dacă poziția $K$ este impară atunci numărul căutat este egal cu $(N+K-R)$ sau $N$ dacă acest rest este 0. Dacă poziția $K$ este pară, atunci numărul căutat este egal cu $(K+R)$ sau $N$ dacă acest rest este 0.

3. Dacă numărul $T$ este par atunci poziția acestui număr în șirul “$A$ sortat” este $poz = (N+T-R)$. Altfel, $poz = (T+R)$. În ambele situații, dacă $poz=0$ atunci $poz=N$. Cunoscând poziția lui $T$ în șirul “$A$ sortat”, determinăm numerele situate pe poziția $poz-1$ (sau $N$) pentru predecesor, respectiv $poz+1$ (sau 1) pentru succesor folosindu-ne de rezultatele menționate mai sus.

Detaliu de implementare: vom folosi faptul că $(x$ este echivalent cu $(x - 1)$, pentru $x > 0$. Demonstrație:

1. $x$, atunci $(x - 1)$.
2. $x$, atunci $(x - 1)$

Sursa de 100 de puncte:

#include <fstream>
using namespace std;

ifstream fin("asort.in");
ofstream fout("asort.out");

int r, n;

int pozToNumber(int poz) {
    if (((poz % 2 == 0) ^ (r % 2 == 0)) == 0) {  // ambele sau niciuna
        return (r + poz - 1) % n + 1;
    } else {
        return (n + poz - r - 1) % n + 1;
    }
}

int numberToPoz(int nr) {
    if (nr % 2 == 0) {
        return (n + nr - r - 1) % n + 1;
    } else {
        return (nr + r - 1) % n + 1;
    }
}

void calcAnswer() {
    int cer, t, k, poz, val, pred, succ;
    fin >> cer >> n >> r >> k >> t;
    r %= n;  // la n operatii se revine la sirul initial

    if (cer == 1) {
        fout << pozToNumber(k) << "\n";
    } else {
        poz = numberToPoz(t);
        pred = pozToNumber(poz == 1 ? n : poz - 1);  // predecesorul
        succ = pozToNumber(poz == n ? 1 : poz + 1);  // succesorul
        fout << pred << " " << succ << "\n";
    }
}

int main() {
    calcAnswer();
    return 0;
}

Probleme rezolvate

Problema Robinson

View Problem

Kilonova

Could not fetch problem details

Deschide

Mai intai, vom construi matricea in modul descris. Dupa aceea, va trebuie sa simulam drumul din problema. Pentru a afla usor urmatoarea pozitie, vom folosi vectori de directie. După ce aflăm directța în care mergem, vom marca poziția ca vizitată (adică setăm valoarea din matrice la $VISITED$, o constantă care va fi egală cu $-1$ sau cu orice valoare care nu poate apărea in matrice).

De asemenea, pentru a determina ușor dacă am ieșit sau nu din matrice, vom borda matricea cu valoarea $VISITED$.

Sursa de 100 de puncte:

#include <fstream>
using namespace std;

ifstream fin("robinson.in");
ofstream fout("robinson.out");

const int MAXM = 100;
const int VISITED = -1;
const int N_DIR = 4;  // cate directii sunt

int n, m, l, c, mat[MAXM + 2][MAXM + 2];
int dx[N_DIR] = {-1, 0, 1, 0},
    dy[N_DIR] = {0, 1, 0, -1};  // vectori de directie

void calcMatrix() {
    int i, j;
    fin >> m >> n >> l >> c;
    for (i = 1; i <= m; i++) {
        mat[1][i] = mat[i][1] = n + i - 1;
    }
    for (i = 2; i <= m; i++) {
        for (j = 2; j <= m; j++) {
            // pastram ultimele trei cifre
            mat[i][j] = (mat[i - 1][j] + mat[i][j - 1]) % 1000;
        }
    }
    fout << mat[m][m] << "\n";
}

void borderMatrix() {
    int i;
    for (i = 0; i <= m + 1; i++) {
        mat[0][i] = mat[m + 1][i] = mat[i][0] = mat[i][m + 1] = VISITED;
    }
}

void simulateProcess() {
    int gata = 0, dir;
    while (!gata) {
        fout << l << " " << c << "\n";
        dir = mat[l][c] % N_DIR;
        mat[l][c] = VISITED;

        l += dx[dir];  // avansam catre urmatoarea pozitie
        c += dy[dir];
        if (mat[l][c] == VISITED) {  // conditia de oprire
            gata = 1;
        }
    }
}

int main() {
    calcMatrix();
    borderMatrix();  // bordarea matricei
    simulateProcess();
    return 0;
}

Problema Furnica

View Problem

Kilonova

Could not fetch problem details

Deschide

În această problemă este destul de direct ce trebuie să facem. Vom simula procesul descris, ținând o matrice $fr\_{i, j}$ care va reprezenta de câte ori am trecut printr-o anumită poziție $(i, j)$. De asemenea, și în această problemă vom folosi vectori de direcție pentru a afla ușor următoarea poziție.

#include <fstream>
using namespace std;

ifstream fin("furnica.in");
ofstream fout("furnica.out");

const int MAXN = 100;
const int N_DIR = 8;

int fr[MAXN][MAXN], n;

// vectori de directie
int dlin[N_DIR] = {-1, -1, 0, 1, 1, 1, 0, -1};
int dcol[N_DIR] = {0, 1, 1, 1, 0, -1, -1, -1};

void visitPositions() {
    int k, l, c, dir;
    fin >> n >> k;

    l = c = 0;
    fr[0][0] = 1;
    for (; k > 0; k--) {
        fin >> dir;
        l += dlin[dir - 1];
        c += dcol[dir - 1];
        fr[l][c]++;
    }
}

void calcAnswer() {
    int sum, i, j, maxim, cnt;
    sum = maxim = cnt = 0;
    for (i = 0; i < n; i++) {
        for (j = 0; j < n; j++) {
            if (fr[i][j] > 0) {
                sum += (i + j + 2) % 6;
                if (fr[i][j] > maxim) {
                    maxim = fr[i][j];
                    cnt = 1;
                } else if (fr[i][j] == maxim) {
                    cnt++;
                }
            }
        }
    }
    fout << sum << " " << cnt << "\n";
}

int main() {
    visitPositions();
    calcAnswer();
    return 0;
}

Concluzii

În problemele de simulare, de obicei, este destul de ușor să îți dai seama ce trebuie să faci, dar implementarea, uneori, nu este așa de ușoară precum pare. Pentru ca implementările a acestor probleme să vi se pară mai ușoare, recomandăm să rezolvați cât mai multe probleme de implementare/simulare, eventual și unele la care este de scris mai mult.

Problemele de optimizare sunt, în mare parte, din categoriile prezentate. Dar, la unele probleme, sunt necesare alte observații care duc la o optimizare mai puțin obișnuită. De aceea, trebuie să fim mereu foarte atenți la detalii și să facem toate observațiile necesare.

Probleme suplimentare

• joc - ONI 2011 VI
• furnica - OJI 2007 VI
• oua - ONI 2007 VI
• circular - OJI 2022 X
• gcl - Baraj 2018 Juniori (O problemă la care este mult de scris, dar care vă ajută să vă organizați codul mai bine și vă îmbunătățește abilitățile de implementare)
• medalion - ONI 2012 VI (Trebuie să simulați cum se construiește o spirală)
• tinta - ONI 2014 VI
• robinhood - ONI 2024 V
• numere - OJI 2008 V (necesită cunoștința perioadei Pisano)
• cartofi - OJI 2021 VIII
• seif - Lot 2022 Juniori
• loopover - Lot 2022 Juniori
• Probleme de forță brută de pe kilonova
• Probleme de periodicitate de pe kilonova
• Alte probleme de implementare de pe kilonova

Resurse suplimentare

• Simulation - USACO Guide
• Verificarea unor proprietati - pbinfo
• Simulare - algopedia
• Simulare, partea 2 - algopedia