Principiul includerii și excluderii (pinex)

În unele probleme de algoritmică, suntem nevoiți să calculăm numărul de răspunsuri care se potrivesc cu o anumită regulă, dar numărarea directă a fiecărei reguli în mod individual nu aduce cu ușurință răspunsul corect. În cazul acestor probleme, vom apela la un principiu matematic folosit în foarte mulți algoritmi elementari studiați până acum, formalizând discuția și aducând mai multe asemenea probleme în discuție.

Definiție

Principiul includerii și al excluderii (de asemenea denumit pinex) este un principiu matematic care este folosit atunci când vrem să aflăm reuniunea a două sau mai multe mulțimi, generalizându-se modul de calculare a răspunsurilor pentru această clasă de probleme.

Cu alte cuvinte, dacă avem două sau mai multe condiții care se intersectează, vrem să evităm numărarea de mai multe ori a unor elemente. Vom pleca de la exemple simple pentru a putea generaliza mai ușor.

Aplicarea PINEX pentru două mulțimi

Dacă avem două mulțimi $A$ și $B$ , pentru a afla numărul de valori care se regăsesc în cel puțin una dintre mulțimi putem să scădem din suma cardinalelor lui $A$ și $B$ , cardinalul intersecției celor două mulțimi. Mai formal, vom avea următoarea formulă:

$|A \cup B| = |A| + |B| - |A \cap B|$

Se poate observa că versiuni rudimentare ale acestei tehnici au fost folosite și în cazul calculării unor răspunsuri pe baza sumelor parțiale (suma valorilor de la poziția $L$ la $R$ este suma primelor $R$ valori din care scădem suma primelor $L-1$ valori) sau în cazul unor alte probleme celebre.

Problema MooBuzz

View Problem

USACO

Deschide

Această problemă este o adaptare a celebrei probleme FizzBuzz, cerându-se aflarea celui de-al $n$ -lea număr scris pe tablă. Pentru a face acest lucru, vom putea căuta binar răspunsul, știind că la fiecare pas, putem afla câte numere au fost scrise pe tablă care sunt mai mici sau egale cu $k$ .

Pentru aflarea acestui răspuns, vom avea două mulțimi:

$A = \{x | x \ % \ 3 = 0, x \leq k }$
$B = \{x | x \ % \ 5 = 0, x \leq k }$

Este evident că vom scădea din $|A| + |B|$ valoarea $|A \cap B|$ , care reprezintă mulțimea numerelor care se împart la 15, soluția devenind una în timp constant, singurul factor de timp prezent fiind cel corespunzător căutării binare. Mai jos puteți găsi implementarea în limbajul C++.

#include <fstream>
using namespace std;

int main() {
    ifstream cin("moobuzz.in");
    ofstream cout("moobuzz.out");

    int n;
    cin >> n;

    long long L = 1;
    long long R = 2000000000;
    long long ans = 0;

    while (L <= R) {
        long long mid = (L + R) / 2;
        long long cnt = mid / 3 + mid / 5 - mid / 15;
        if (mid - cnt >= n) {
            ans = mid;
            R = mid - 1;
        } else {
            L = mid + 1;
        }
    }

    cout << ans << '\n';
    return 0;
}

Aplicarea PINEX pentru trei sau mai multe mulțimi

Pentru a aplica aceeași formulă pentru trei sau mai multe mulțimi, vom prezenta o proprietate importantă care ne va ajuta de-a lungul formulelor viitoare.

Observație

Pentru a calcula răspunsul unei probleme la care va trebui să aplicăm acest principiu, vom aduna mereu la răspuns numărul elementelor care se află într-un număr impar de mulțimi și vom scădea din răspuns cele care apar într-un număr par de mulțimi.

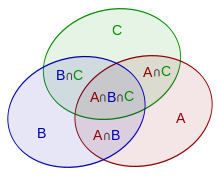
De exemplu, când avem trei mulțimi, formula de mai devreme devine

|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C|

În mod general, dacă avem $k$ mulțimi, răspunsul va deveni următorul, unde $A\_i$ reprezintă cea de-a $i$ -a mulțime:

\left| \bigcup_{i=1}^n A_i \right| = \sum_{i=1}^n|A_i| - \sum_{1\leq i<j\leq n} |A_i \cap A_j| + \sum _{1\leq i<j<k\leq n}|A_i \cap A_j \cap A_k| - \cdots + (-1)^{n-1} | A_1 \cap \cdots \cap A_n |

Pe scurt, formula va deveni următoarea:

\bigg|\bigcup_{i=1}^nA_i \bigg|= \sum_{0 \neq J \in \{1, 2,...,n\} } (-1)^{|J|-1} \bigg| \bigcap_{j \in J} A_j \bigg|

Acest lucru ne garantează că pentru un element care apare în mai multe mulțimi, deși este adunat individual de mai multe ori, se scad părțile care apar în plus în calculul final.

Observație

Dacă avem de-a face cu o problemă la care trebuie să recurgem la aflarea complementului răspunsului folosind PINEX, termenii care se adună și cei care se scad se inversează.

Problema Prime Multiples

View Problem

CSES

Deschide

Pentru a afla câte valori se împart la măcar unul din cele $n$ numere prime date, vom afla pentru fiecare submulțime de numere câte numere se împart la produsul numerelor din submulțime, adunând sau scăzând din răspuns după caz. Pentru a face asta ușor, vom reprezenta fiecare submulțime folosind o mască pe biți, tehnică explicată în acest articol. Singurul lucru la care trebuie avut grijă este obținerea produselor submulțimilor, pentru a evita overflow-urile.

#include <iostream>
#include <vector>

using namespace std;

int main() {
    long long n, k;
    cin >> n >> k;

    vector<long long> v(k);
    for (int i = 0; i < k; ++i) {
        cin >> v[i];
    }

    long long sum = 0;
    for (int msk = 1; msk < (1 << k); ++msk) {
        long long prod = 1;
        int cnt = 0;
        for (int i = 0; i < k; ++i) {
            if (msk & (1 << i)) {
                if (n / prod < v[i]) {  // evitam overflowul
                    prod = n + 1;
                } else {
                    prod = prod * v[i];
                }
                ++cnt;
            }
        }
        if (cnt % 2 == 1) {
            sum += n / prod;
        } else {
            sum -= n / prod;
        }
    }

    cout << sum;
    return 0;
}

Aplicarea PINEX în probleme mai complexe

Pe lângă aplicarea funcției Möbius în problemele dificile ce folosesc PINEX, se mai regăsește o formă de aplicare a acestui principiu, atunci când trebuie să numărăm câte perechi sau mulțimi de valori au o anumită valoare a unei funcții. De foarte multe ori, funcțiile ce apar în aceste probleme sunt multiplicative, deci scopul va fi acela de a exclude mulțimile care au drept răspuns o valoare multiplu de numărul pe care îl căutăm.

Problema Counting Coprime Pairs

View Problem

CSES

Deschide

Pentru a afla numărul de perechi de numere prime între ele, vom afla pentru fiecare valoare posibilă a celui mai mare divizor comun câte asemenea perechi există. Pentru a face acest lucru, vom itera în ordine descrescătoare și vom afla mai întâi numărul de numere multiple cu $i$ din șirul dat, iar mai apoi vom scădea din numărul de perechi posibile care se pot genera, numărul de perechi deja aflate la pașii anteriori, când am verificat valori mai mari ale celui mai mare divizor comun. Mai jos se poate vedea o asemenea implementare.

#include <iostream>
#include <vector>

using namespace std;

int main() {
    vector<long long> fr(1000001), cnt(1000001);

    int n;
    cin >> n;

    for (int i = 1; i <= n; ++i) {
        int val;
        cin >> val;
        fr[val]++;
    }

    long long ans = 1LL * n * (n - 1) / 2;
    for (int i = 1000000; i >= 2; --i) {
        long long val = 0;
        // aflam cate valori sunt multipli de i
        for (int j = i; j <= 1000000; j += i) {
            val += fr[j];
        }
        cnt[i] = val * (val - 1) / 2;
        // scadem perechile deja calculate
        for (int j = i + i; j <= 1000000; j += i) {
            cnt[i] -= cnt[j];
        }
        ans -= cnt[i];
    }

    cout << ans;
    return 0;
}

Problemă rezolvată - Lot 2024 Juniori pmo

Mai întâi, vom fixa numărul de factori din produs. Fie acesta $i$ . Putem observa că $i$ este mai mic sau egal cu suma exponenților din descompunerea în factori primi a lui $x$ (să notăm această sumă cu $S$ ). Noi nu putem să ne asigurăm ca fiecare număr va fi mai mare ca 1 decât dacă ne asigurăm că fiecare număr are toate numerele prime din descompunerea lui $x$ în descompunerea lui.

Noi vrem ca exact 0 din cele $i$ elemente să fie egale cu 1. Pentru a calcula acest număr, putem aplica PINEX în funcție de câte elemente am fixat să fie egale cu 1.

Fie $f(n, i)$ numărul de moduri de a împărți numărul $n$ în produs de $i$ elemente, care pot fi și egale cu 1.

Răspunsul va fi $\sum \_{i=1} ^S \sum \_{j=0} ^i \ (-1)^j \cdot C \_i ^j \cdot f(x, i-j)$ , deoarece putem alege cele $j$ elemente care vor fi egale cu 1 în $C \_i ^j$ moduri.

Observație

Să calculam $f(n, i)$ . Fie $k$ numărul de factori primi ai lui $n$ și fie $exp\_k$ exponentul al celui de-al $k$ -lea factor prim în $n$ . Pentru a afla numărul, putem să ne legăm de fiecare factor prim. Noi trebuie sa vedem câți vectori (tablouri unidimensionale) de lungime $i$ cu elemente posibil nule au suma elementelor egală cu $exp\_K$ . Această formulă este studiată în articolul de Stars and Bars. Așa că, numărul căutat va fi $\prod \_{j=1} ^k C \_{exp_k+i-1} ^{i-1}$ .

Observație

Descompunerea în factori primi o vom face folosind numerele prime, pe care le vom precalcula folosind ciurul lui Eratostene.

Observație

Unele calcule pot fi foarte mari, mai mari decât poate stoca tipul long long. De aceea, vom folosi \__int128.

Sursa de 100 de puncte:

#include <algorithm>
#include <fstream>
#include <string>

std::ifstream fin("pmo.in");
std::ofstream fout("pmo.out");

std::istream &operator>>(std::istream &in, __int128 &n) {
    int i;
    std::string s;
    in >> s;
    n = 0;
    for (i = 0; i < (int)s.size(); i++) {
        n = n * 10 + s[i] - '0';
    }
    return in;
}

std::ostream &operator<<(std::ostream &out, __int128 n) {
    std::string s = "";
    do {
        s.push_back('0' + n % 10);
        n /= 10;
    } while (n > 0);
    std::reverse(s.begin(), s.end());
    out << s;
    return out;
}

const int MAXP = 32'000;
const int MAXEXPS = 64;

char ciur[MAXP];
int prime[MAXP], exps[MAXEXPS], sumexp, nfact;
long long comb[MAXEXPS][MAXEXPS];
__int128 ways[MAXEXPS];  // ways[i] = nrmod de a scrie x ca prod de i nr

void precomputeSieve() {
    int i, j;
    for (i = 2; i * i < MAXP; i++) {
        if (ciur[i] == 0) {
            for (j = i * i; j < MAXP; j += i) {
                ciur[j] = 1;
            }
        }
    }
}

void precomputePrimes() {
    int i, p;
    p = 0;
    for (i = 2; i < MAXP; i++) {
        if (ciur[i] == 0) {
            prime[p++] = i;
        }
    }
}

void precomputeComb() {
    int i, j;
    comb[0][0] = 1;
    for (i = 1; i < MAXEXPS; i++) {
        comb[i][0] = 1;
        for (j = 1; j <= i; j++) {
            comb[i][j] = comb[i - 1][j] + comb[i - 1][j - 1];
        }
    }
}

void precompute() {
    precomputeSieve();
    precomputePrimes();
    precomputeComb();
}

void decomposeInPrimes(int val) {
    int i;
    nfact = i = sumexp = 0;
    while (prime[i] * prime[i] <= val) {
        if (val % prime[i] == 0) {
            exps[nfact] = 0;
            do {
                exps[nfact]++;
                val /= prime[i];
            } while (val % prime[i] == 0);
            sumexp += exps[nfact++];
        }
        i++;
    }
    if (val > 1) {
        exps[nfact++] = 1;
        sumexp++;
    }
}

long long starsAndBars(int n, int k) { return comb[n + k - 1][k - 1]; }

void computeWays() {
    int i, j;
    for (i = 0; i <= sumexp; i++) {
        ways[i] = 1;
        for (j = 0; j < nfact; j++) {
            ways[i] *= starsAndBars(exps[j], i);
        }
    }
}

void calcAnswer() {
    int i, j;
    __int128 answer, prod;
    answer = 0;
    for (i = 1; i <= sumexp; i++) {
        for (j = 0; j < i; j++) {
            prod = comb[i][j] * ways[i - j];
            if (j % 2 == 0) {
                answer += prod;
            } else {
                answer -= prod;
            }
        }
    }
    fout << answer << "\n";
}

void answerQueries() {
    int t, x;
    fin >> t;
    while (t--) {
        fin >> x;
        decomposeInPrimes(x);
        computeWays();
        calcAnswer();
    }
}

int main() {
    precompute();
    answerQueries();
    return 0;
}

Concluzii

Principiul includerii și excluderii este un principiu ce se dovedește a fi util în foarte multe probleme de numărare, cunoașterea acestuia dovedindu-se a fi esențială în multe probleme, începând de la concursurile de juniori (lot, concursuri internaționale) și terminând cu diverse competiții online în care teoria numerelor își face apariția. Mai târziu, funcții sau constante ce se bazează pe PINEX vor demonstra o dată în plus utilitatea acestui principiu. Problemele de mai jos pot avea și alte abordări, în afară de cea cu PINEX, toate fiind foarte utile și folositoare în competițiile de informatică.

Principiul includerii și excluderii (pinex)

Aplicarea PINEX pentru două mulțimi

Problema MooBuzz

View Problem

Aplicarea PINEX pentru trei sau mai multe mulțimi

Problema Prime Multiples

View Problem

Aplicarea PINEX în probleme mai complexe

Problema Counting Coprime Pairs

View Problem

Problemă rezolvată - Lot 2024 Juniori pmo

Concluzii

Probleme suplimentare

Lectură suplimentară

On this page